12. Sınıf Fizik
Ünite: Elektrik ve Manyetizma
Konu: Direnç ve Ohm Kanunu
1. Elektrik Akımı ve Direncin Temelleri
Bir iletken tel boyunca elektrik akımı geçtiğinde, tel içindeki serbest elektronlar yönlü hareket eder. Ancak bu hareket sırasında elektronlar, iletkenin atomlarıyla çarpışır. Bu çarpışmalar, elektronların akışını yavaşlatır ve enerjilerinin bir kısmı ısıya dönüşür. Elektron akışına karşı gösterilen bu zorluk elektrik direnci (R) olarak adlandırılır.
Direnç, akımın geçişine karşı gösterilen engeldir. Yani bir devrede direnç ne kadar büyükse, akım o kadar küçük olur.
2. Direncin Tanımı ve Birimi
Tanım:
Elektrik akımına karşı iletkenin gösterdiği zorluk miktarına direnç denir.
Matematiksel olarak, direnç ile gerilim ve akım arasındaki ilişki Ohm Kanunu ile belirlenir: R=VIR = \frac{V}{I}R=IV
Burada:
- R → Direnç (ohm, Ω)
- V → Gerilim (volt, V)
- I → Akım (amper, A)
Yani bir devredeki gerilim (V) biliniyorsa ve akım (I) ölçülmüşse, bu değerlerin oranı dirençtir.
3. Ohm Kanunu
Ohm Kanunu (Ohm Yasası), Alman fizikçi Georg Simon Ohm tarafından 1827’de formüle edilmiştir. Bu yasa, elektrik devrelerinin temelini oluşturur.
Bir iletkenden geçen akım, uygulanan gerilimle doğru; iletkenin direnciyle ters orantılıdır.
Formül: I=VRI = \frac{V}{R}I=RV
Bu ifade, bir iletkene uygulanan gerilim iki katına çıkarıldığında, akımın da iki katına çıkacağını; direncin artması durumunda ise akımın azalacağını gösterir.
Ohm Kanunu sadece Ohmik iletkenler için geçerlidir.
4. Ohmik ve Ohmik Olmayan Maddeler
🔹 Ohmik Maddeler:
- Akım–gerilim grafiği doğru şeklindedir.
- Direnç, gerilime ve akıma bağlı olarak değişmez (sabit kalır).
- Örnek: Metal teller, karbon dirençler, iletken teller.
🔹 Ohmik Olmayan Maddeler:
- Akım–gerilim grafiği doğrusal değildir.
- Direnç sabit kalmaz, gerilime bağlı olarak değişir.
- Örnek: Diyot, lamba teli, transistör, LED.
5. Akım – Gerilim Grafiği
Ohm kanununa göre I=VRI = \frac{V}{R}I=RV olduğundan:
- Gerilim arttıkça akım artar.
- Eğer R sabitse, bu artış doğrusal olur.
Grafik:
Yatay eksende gerilim (V), dikey eksende akım (I) alınır.
- Doğru çizgi elde edilirse madde ohmiktir.
- Eğri çizgi elde edilirse ohmik değildir.
Eğim ilişkisi: Eg˘im=VI=R\text{Eğim} = \frac{V}{I} = REg˘im=IV=R
Yani doğrunun eğimi, iletkenin direncini verir.
6. Direncin Bağlı Olduğu Faktörler
Bir iletkenin direnci sabit bir değer değildir; telin fiziksel özelliklerine bağlı olarak değişir.
Direnç şu formülle ifade edilir: R=ρLAR = \rho \frac{L}{A}R=ρAL
Burada:
- R: Direnç (Ω)
- ρ (rho): Maddenin özdirenci (Ω·m)
- L: Telin uzunluğu (m)
- A: Telin kesit alanı (m²)
a) Uzunluk (L)
İletkenin uzunluğu arttıkça, elektronlar daha fazla atomla çarpışır → direnç artar.
R ∝ L
b) Kesit Alanı (A)
Telin kalınlığı arttıkça, elektronlar için daha geniş bir yol olur → direnç azalır.
R ∝ 1/A
c) Özdirenç (ρ)
Her maddenin elektrik akımına karşı gösterdiği doğuştan gelen zorluk farklıdır. Bu özelliğe özdirenç denir.
- Bakır ve gümüş gibi iletkenlerde ρ küçüktür.
- Nikel, demir gibi maddelerde ρ büyüktür.
d) Sıcaklık
Genellikle sıcaklık arttıkça direnç de artar. Çünkü atomlar daha hızlı titreşir, elektronların hareketi zorlaşır.
Ancak bazı özel maddelerde (yarı iletkenlerde) sıcaklık arttıkça direnç azalabilir.
7. Direnç Birimi
Direnç birimi ohm (Ω)’dur.
Tanım olarak:
Bir iletkene 1 voltluk gerilim uygulandığında, 1 amperlik akım geçiyorsa o iletkenin direnci 1 ohm’dur.
1 Ω=1 V1 A1\,Ω = \frac{1\,V}{1\,A}1Ω=1A1V
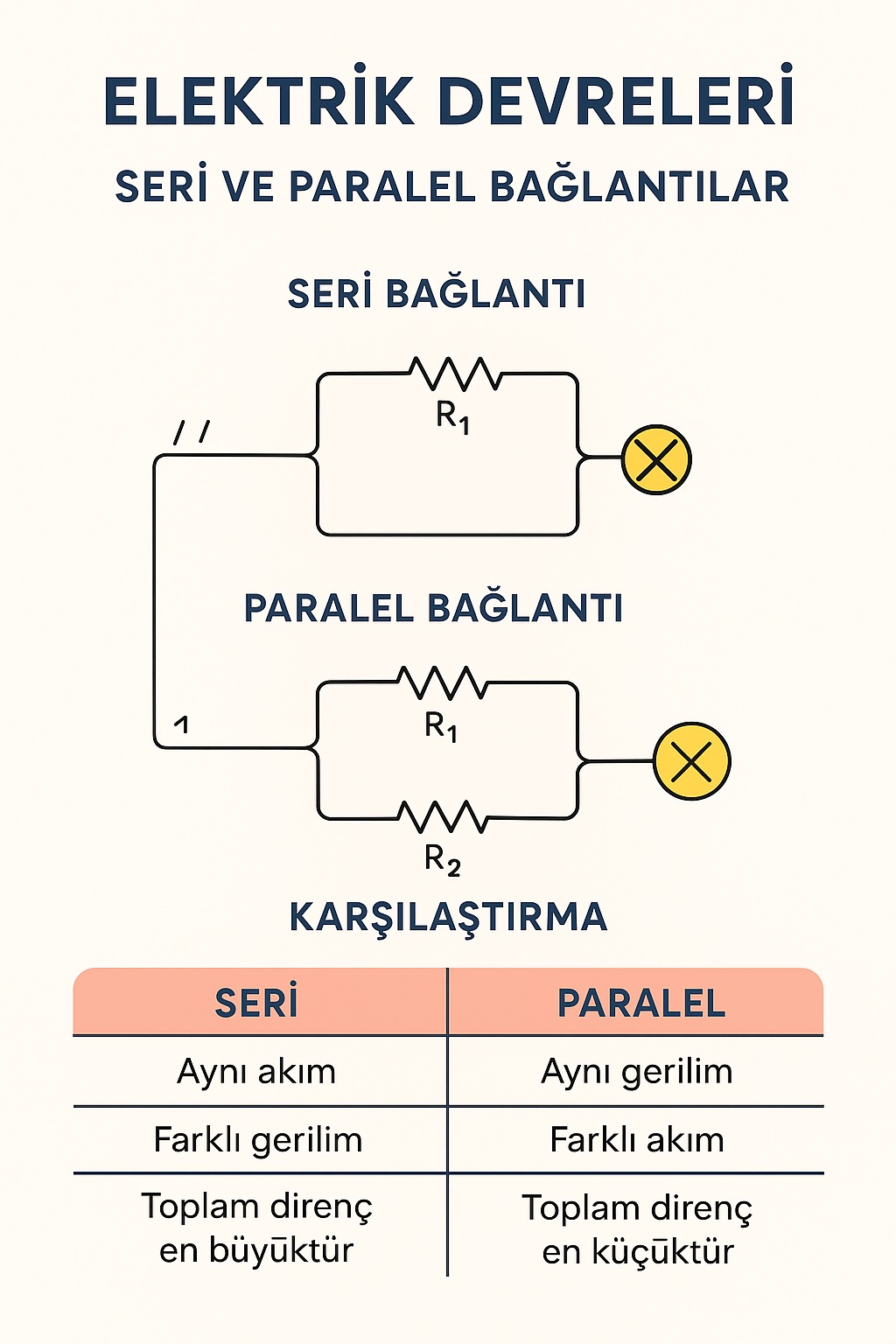
8. Seri ve Paralel Direnç Bağlantıları
Bir devrede birden fazla direnç kullanıldığında, bunlar seri, paralel ya da karma bağlanabilir.
🔹 A) Seri Bağlantı
Dirençler uç uca bağlanır; akımın geçtiği yol tektir.
- Akım (I) her noktada aynıdır.
- Gerilim (V) dirençlere göre paylaştırılır.
Toplam direnç: Rt=R1+R2+R3+…R_{t} = R_1 + R_2 + R_3 + \dotsRt=R1+R2+R3+…
Gerilim dağılımı: Vt=V1+V2+V3V_t = V_1 + V_2 + V_3Vt=V1+V2+V3
Akım sabit: I1=I2=I3=ItI_1 = I_2 = I_3 = I_tI1=I2=I3=It
Örnek:
3 Ω, 5 Ω ve 2 Ω’luk dirençler seri bağlanırsa: Rt=3+5+2=10 ΩR_t = 3 + 5 + 2 = 10\,ΩRt=3+5+2=10Ω
🔹 B) Paralel Bağlantı
Dirençlerin uçları aynı iki noktaya bağlanır.
- Gerilim (V) her dirençte aynıdır.
- Akım (I) dirençlere göre paylaşılır.
Toplam direnç: 1Rt=1R1+1R2+1R3\frac{1}{R_t} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}Rt1=R11+R21+R31
Özellik:
Paralel bağlamada toplam direnç, en küçük dirençten bile daha küçük olur.
Örnek:
6 Ω ve 3 Ω direnç paralel bağlanırsa: 1Rt=16+13=12⇒Rt=2 Ω\frac{1}{R_t} = \frac{1}{6} + \frac{1}{3} = \frac{1}{2} \Rightarrow R_t = 2\,ΩRt1=61+31=21⇒Rt=2Ω
🔹 C) Karma (Bileşik) Bağlantı
Bazı devrelerde hem seri hem paralel bağlantılar bir aradadır. Bu tür devrelerde önce paralel, sonra seri (ya da tersi) işlemleri adım adım yapılarak toplam direnç bulunur.
9. Elektrik Gücü ve Enerjisi
Direnç üzerinden akım geçtiğinde, enerji ısıya dönüşür. Bu olay Joule Yasası ile açıklanır.
Güç formülü: P=V⋅IP = V \cdot IP=V⋅I
Ayrıca: P=I2RveP=V2RP = I^2 R \quad \text{ve} \quad P = \frac{V^2}{R}P=I2RveP=RV2
Enerji formülü: E=P⋅tE = P \cdot tE=P⋅t
Burada:
- P: Güç (Watt, W)
- E: Enerji (Joule, J)
- t: Zaman (s)
Günlük yaşamda: Elektrik sayaçları kilowatt-saat (kWh) birimini kullanır. 1 kWh=3.6×106 J1\,kWh = 3.6 \times 10^6\,J1kWh=3.6×106J
10. Dirençlerin Isıl Etkisi (Joule Yasası)
Direnç üzerinden geçen akım, iletkenin içinde ısı üretir.
Bu ısı miktarı: Q=I2RtQ = I^2 R tQ=I2Rt
- Akım (I) iki katına çıkarsa ısı 4 kat artar.
- Direnç artarsa ısı artar.
- Zaman uzadıkça ısı miktarı artar.
Bu etki, elektrikli soba, ütü, ampul gibi cihazlarda kullanılır.
11. Örnek Problemler
🧩 Örnek 1:
Bir devrede 12 V gerilim uygulanıyor ve 4 A akım geçiyorsa, devre direncini bulun. R=VI=124=3 ΩR = \frac{V}{I} = \frac{12}{4} = 3\,ΩR=IV=412=3Ω
🧩 Örnek 2:
10 Ω’luk bir dirençten 2 A akım geçmektedir. Bu dirençteki güç ve harcanan enerjiyi (5 saniyede) bulun. P=I2R=22⋅10=40 WP = I^2 R = 2^2 \cdot 10 = 40\,WP=I2R=22⋅10=40W E=P⋅t=40⋅5=200 JE = P \cdot t = 40 \cdot 5 = 200\,JE=P⋅t=40⋅5=200J
🧩 Örnek 3:
Bir devrede 3 Ω, 6 Ω ve 9 Ω dirençler paralel bağlanmıştır. Toplam direnç: 1Rt=13+16+19=1118⇒Rt=1.64 Ω\frac{1}{R_t} = \frac{1}{3} + \frac{1}{6} + \frac{1}{9} = \frac{11}{18} \Rightarrow R_t = 1.64\,ΩRt1=31+61+91=1811⇒Rt=1.64Ω
12. Gerçek Dirençlerin Özellikleri
Gerçek dirençler sadece akıma karşı koymakla kalmaz, aynı zamanda ısı üretirler.
Bu nedenle:
- Direnç arttıkça enerji kaybı artar.
- Verim düşer.
- Elektronik devrelerde enerji tasarrufu için düşük ısı yayan dirençler tercih edilir.
Dirençler genellikle renk kodlarıyla tanımlanır. Her renk bir rakamı ifade eder, bu sayede direnç değeri kolayca okunabilir.
13. Direnç Renk Kodları
Dirençlerin üzerinde 4, 5 veya 6 renkli bant bulunur. Bu bantlar direnç değerini belirtir.
| Renk | Sayı | Çarpan | Tolerans |
|---|---|---|---|
| Siyah | 0 | 1 | – |
| Kahverengi | 1 | 10 | ±1% |
| Kırmızı | 2 | 100 | ±2% |
| Turuncu | 3 | 1.000 | – |
| Sarı | 4 | 10.000 | – |
| Yeşil | 5 | 100.000 | ±0.5% |
| Mavi | 6 | 1.000.000 | ±0.25% |
| Mor | 7 | 10⁷ | ±0.1% |
| Gri | 8 | 10⁸ | ±0.05% |
| Beyaz | 9 | 10⁹ | – |
| Altın | – | 0.1 | ±5% |
| Gümüş | – | 0.01 | ±10% |
14. Direncin Sıcaklıkla Değişimi
Metallerde sıcaklık arttıkça atom titreşimleri artar → elektronların geçişi zorlaşır → direnç artar.
Formül: RT=R0[1+α(T−T0)]R_T = R_0 [1 + \alpha (T – T_0)]RT=R0[1+α(T−T0)]
Burada:
- R0R_0R0: Başlangıç direnci
- RTR_TRT: T sıcaklığındaki direnç
- α\alphaα: Direnç sıcaklık katsayısı
- T,T0T, T_0T,T0: Sıcaklıklar (°C)
15. Günlük Hayatta Direnç ve Ohm Kanunu
Direnç ve Ohm Yasası günlük yaşamda birçok teknolojide temel rol oynar:
- Ev aydınlatması: Ampullerin parlaklığı dirence göre belirlenir.
- Isıtıcılar ve fırınlar: Elektrik enerjisi dirençte ısıya dönüşür.
- Elektronik devreler: Akımı sınırlamak için dirençler kullanılır.
- Araç sistemleri: Sensörler ve kontrol devreleri Ohm yasasına göre çalışır.
16. Özet
| Büyüklük | Sembol | Birim | Formül | Açıklama |
|---|---|---|---|---|
| Gerilim | V | Volt (V) | V=I⋅RV = I·RV=I⋅R | Potansiyel farkı |
| Akım | I | Amper (A) | I=V/RI = V/RI=V/R | Elektron akışı |
| Direnç | R | Ohm (Ω) | R=V/IR = V/IR=V/I | Akıma karşı zorluk |
| Güç | P | Watt (W) | P=VIP = VIP=VI | Enerji dönüşüm hızı |
| Enerji | E | Joule (J) | E=P⋅tE = P·tE=P⋅t | Toplam iş miktarı |
Direnç ve Ohm Kanunu, elektrik devrelerinin temelini oluşturan en önemli fiziksel ilişkidir.
Bu kanun sayesinde devre elemanları arasındaki akım, gerilim ve direnç ilişkisi açıkça hesaplanabilir.
Elektronikten enerji mühendisliğine kadar tüm teknolojik sistemler bu yasaya dayanır.
Direnç kavramını anlamak, elektrik akımının davranışını kavramak açısından büyük önem taşır. Bu bilgiler, ileride elektromanyetizma, alternatif akım, devre analizi, güç sistemleri gibi konuların anlaşılmasına da temel oluşturur.