ELEKTRİK KUVVETİ (COULOMB YASASI) – 10. SINIF FİZİK DERSİ

1. Elektriksel Etkileşim Nedir?

Doğada cisimler birbirine temas etmeden de kuvvet uygulayabilir.
Örneğin:

Dünya ile Ay arasında kütle çekim kuvveti vardır.
Mıknatıslar arasında manyetik kuvvet vardır.
Yüklü cisimler arasında da elektriksel kuvvet bulunur.

Bu kuvvetler, cisimler arasında alan aracılığıyla etki eder.
Elektrik yükleri arasındaki bu çekme veya itme kuvvetine elektriksel kuvvet denir.

2. Elektrik Yükü ve Temel Özellikleri

Elektriksel kuvvetin kaynağı, maddelerin sahip olduğu elektrik yükleridir.
Hatırlayalım:

Proton (+) → pozitif yüklüdür.
Elektron (−) → negatif yüklüdür.
Nötron (0) → yüksüzdür.

Atomlar normalde nötrdür, çünkü proton sayısı = elektron sayısıdır.
Ancak bir atom elektron kaybeder veya kazanırsa, yüklenmiş hale gelir.

Yükün birimi: Coulomb (C)
Simgesi: qqq

Bir elektronun yükü: e=−1.6×10−19 Ce = -1.6 \times 10^{-19} \, \text{C}e=−1.6×10−19C

Bir protonun yükü: p=+1.6×10−19 Cp = +1.6 \times 10^{-19} \, \text{C}p=+1.6×10−19C

3. Elektriksel Kuvvetin Doğası

Yüklü cisimler birbirine iki şekilde kuvvet uygular:

Aynı cins yükler (örneğin + ile +, − ile −) birbirini iter.
Zıt cins yükler (örneğin + ile −) birbirini çeker.

Bu kuvvet, yüklerin büyüklüğüne ve aralarındaki uzaklığa bağlıdır.

Bu bağıntıyı Coulomb Yasası açıklar.

4. Coulomb Yasası Nedir?

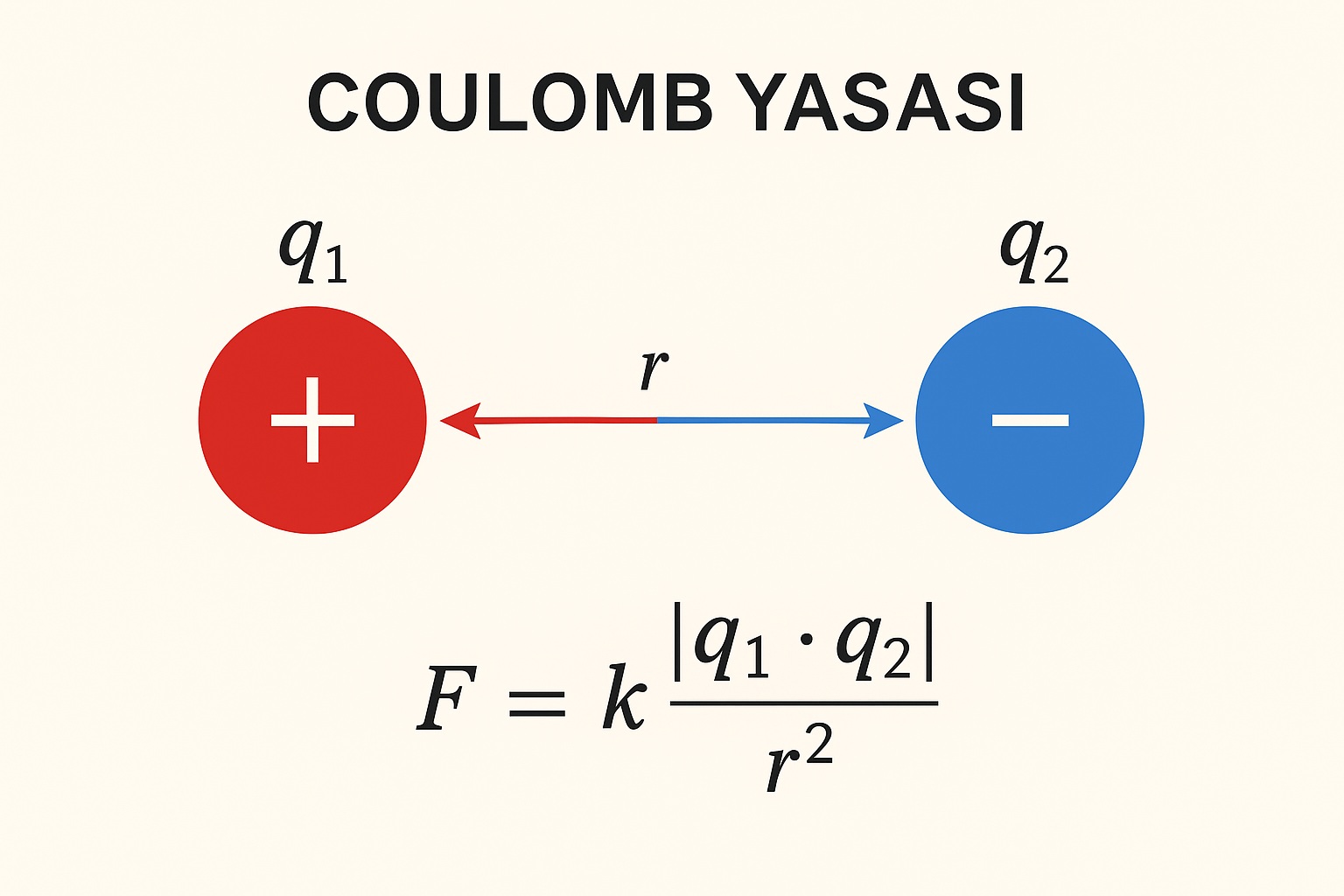
Coulomb Yasası, iki noktasal yük arasındaki elektriksel kuvveti tanımlar.
Yasayı ilk olarak Charles Augustin de Coulomb (1736–1806) deneysel olarak bulmuştur.

Coulomb, dönme terazisi (torsiyon terazisi) kullanarak iki yük arasındaki kuvveti ölçmüş ve şu sonucu elde etmiştir:

İki yük arasındaki elektriksel kuvvetin büyüklüğü, yüklerin çarpımı ile doğru, aralarındaki uzaklığın karesi ile ters orantılıdır.

Matematiksel olarak: F=k∣q1⋅q2∣r2F = k \frac{|q_1 \cdot q_2|}{r^2}F=kr2∣q1⋅q2∣

Burada:

FFF: Yükler arasındaki elektriksel kuvvet (Newton, N)
q1,q2q_1, q_2q1,q2: Elektrik yükleri (Coulomb, C)
rrr: Yükler arasındaki uzaklık (metre, m)
kkk: Coulomb sabiti

5. Coulomb Sabiti (kkk)

Boşlukta veya havada: k=9×109 N\cdotpm2/C2k = 9 \times 10^9 \, \text{N·m}^2/\text{C}^2k=9×109N\cdotpm2/C2

Bu sabit, ortamın elektriksel özelliklerine bağlıdır.
Eğer yükler su, cam veya başka bir ortamda bulunursa, ortamın dielektrik katsayısı (ε) dikkate alınır.

Formül o durumda: F=14πε⋅∣q1q2∣r2F = \frac{1}{4\pi \varepsilon} \cdot \frac{|q_1 q_2|}{r^2}F=4πε1⋅r2∣q1q2∣

Burada ε\varepsilonε, ortamın permitivitesidir.

6. Elektriksel Kuvvetin Yönü

Elektrik kuvveti vektörel bir büyüklüktür.

Aynı yükler → birbirini iter, kuvvet vektörleri birbirinden uzaklaşır.
Zıt yükler → birbirini çeker, kuvvet vektörleri birbirine yönelir.

Yani kuvvetin yönü, yüklerin türüne bağlıdır.
Bu kuvvet, her zaman iki yükü birleştiren doğru üzerindedir.

7. Coulomb Kuvvetinin Özellikleri

Merkezi kuvvettir.
Kuvvet çizgisi yük merkezlerinden geçer.
Etkileşim çift yönlüdür.
Newton’un üçüncü yasasına göre, her iki yük birbirine eşit büyüklükte fakat zıt yönlü kuvvet uygular.
Ortamın etkisine bağlıdır.
Yüklerin bulunduğu ortamın türü (hava, su, yağ vs.) kuvvetin büyüklüğünü değiştirir.
Kuvvet uzaklıkla hızla azalır.
Uzaklık iki katına çıkarsa, kuvvet dörtte bire düşer. (Çünkü F∝1/r2F \propto 1/r^2F∝1/r2)

8. Noktasal Yük Kavramı

Coulomb yasasında kullanılan yükler genellikle noktasal yükler olarak düşünülür.
Yani yüklerin boyutları, aralarındaki uzaklığa göre çok küçüktür.

Gerçek hayatta, yüklerin belirli bir yüzeye veya hacme dağılmış olması mümkündür, ancak temel analizlerde yükler noktasal kabul edilir.

9. Birden Fazla Yük Arasındaki Elektrik Kuvveti (Vektörel Toplama)

Eğer bir yük, birden fazla yükten etkileniyorsa, her bir yükün oluşturduğu kuvvet ayrı ayrı bulunur ve vektörel olarak toplanır.

Bu ilkeye Süperpozisyon İlkesi denir.

Yani: F⃗toplam=F⃗1+F⃗2+F⃗3+…\vec{F}_{\text{toplam}} = \vec{F}_1 + \vec{F}_2 + \vec{F}_3 + …Ftoplam=F1+F2+F3+…

Kuvvetlerin yönleri dikkate alınarak toplama yapılmalıdır.
Bu nedenle, doğrultu ve yön önemli bir rol oynar.

10. Elektriksel Kuvvet ile Kütleçekim Kuvvetinin Karşılaştırılması

Özellik	Elektriksel Kuvvet	Kütle Çekim Kuvveti
Nedeni	Elektrik yükleri	Kütle
Yönü	Çekici veya itici olabilir	Her zaman çekicidir
Büyüklük	Çok güçlüdür	Çok zayıftır
Formül	F=kq1q2r2F = k \frac{q_1 q_2}{r^2}F=kr2q1q2	F=Gm1m2r2F = G \frac{m_1 m_2}{r^2}F=Gr2m1m2
Sabit	k=9×109k = 9×10^9k=9×109	G=6.67×10−11G = 6.67×10^{-11}G=6.67×10−11

Sonuç: Elektriksel kuvvet, kütleçekim kuvvetine göre çok daha büyüktür.

Örneğin, bir proton ve elektron arasındaki elektriksel çekim, aralarındaki kütleçekim kuvvetinden yaklaşık 10³⁹ kat daha güçlüdür!

11. Elektriksel Kuvvetin Hesaplanmasına Örnek

Örnek:
İki yük arasındaki uzaklık r=0.02 mr = 0.02 \, \text{m}r=0.02m,
Yüklerin büyüklükleri q1=+2×10−6 Cq_1 = +2 \times 10^{-6} \, \text{C}q1=+2×10−6C ve q2=−3×10−6 Cq_2 = -3 \times 10^{-6} \, \text{C}q2=−3×10−6C olsun.

Aralarındaki kuvvetin büyüklüğünü bulunuz.

Çözüm:

Formül: F=k∣q1q2∣r2F = k \frac{|q_1 q_2|}{r^2}F=kr2∣q1q2∣

Yerine yazalım: F=(9×109)×(2×10−6)(3×10−6)(0.02)2F = (9 \times 10^9) \times \frac{(2 \times 10^{-6})(3 \times 10^{-6})}{(0.02)^2}F=(9×109)×(0.02)2(2×10−6)(3×10−6) F=9×109×6×10−124×10−4F = 9 \times 10^9 \times \frac{6 \times 10^{-12}}{4 \times 10^{-4}}F=9×109×4×10−46×10−12 F=9×109×1.5×10−8F = 9 \times 10^9 \times 1.5 \times 10^{-8}F=9×109×1.5×10−8 F=135 NF = 135 \, \text{N}F=135N

Sonuç:
Kuvvetin büyüklüğü 135 Newton’dur.
Yükler zıt işaretli olduğundan, birbirini çekerler.

12. Aynı Doğrultudaki Üç Yük Problemi

Örnek:

A, B ve C adında üç noktasal yük doğrusal şekilde sıralanmış olsun.

A yükü: +3 μC+3 \, \mu C+3μC
B yükü: +2 μC+2 \, \mu C+2μC
C yükü: −3 μC-3 \, \mu C−3μC
AB = 2 m, BC = 3 m

Soru:
B noktasındaki yükün net kuvvetini bulunuz.

Çözüm:

A ve B aynı işaretli olduğundan iter. FAB=k∣qAqB∣r2=9×109(3×10−6)(2×10−6)22F_{AB} = k \frac{|q_A q_B|}{r^2} = 9\times10^9 \frac{(3\times10^{-6})(2\times10^{-6})}{2^2}FAB=kr2∣qAqB∣=9×10922(3×10−6)(2×10−6) FAB=13.5 NF_{AB} = 13.5 \, \text{N}FAB=13.5N
C ve B zıt işaretli olduğundan çeker. FCB=9×109(3×10−6)(2×10−6)32F_{CB} = 9\times10^9 \frac{(3\times10^{-6})(2\times10^{-6})}{3^2}FCB=9×10932(3×10−6)(2×10−6) FCB=6 NF_{CB} = 6 \, \text{N}FCB=6N

Kuvvetlerin yönleri zıt olduğundan, Fnet=FAB−FCB=13.5−6=7.5 NF_{\text{net}} = F_{AB} – F_{CB} = 13.5 – 6 = 7.5 \, \text{N}Fnet=FAB−FCB=13.5−6=7.5N

Sonuç:
B yükü net 7.5 N’luk bir itme kuvvetine maruz kalır.

13. Elektrik Alan ve Coulomb Kuvveti Arasındaki İlişki

Coulomb yasası ile elektrik alan kavramı yakından ilişkilidir.

Bir yükün oluşturduğu elektrik alan (E), o noktada birim yüke düşen kuvvettir. E=FqE = \frac{F}{q}E=qF

Yani: F=q⋅EF = q \cdot EF=q⋅E

Eğer bir yük çevresine alan oluşturuyorsa, bu alan diğer yüklerin üzerine kuvvet uygular.
Elektrik alanın yönü, pozitif yüklerden dışarı, negatif yükler yönüne doğrudur.

14. Elektrik Kuvvet Çizgileri

Elektrik alanın etkisini görsel olarak göstermek için elektrik alan çizgileri kullanılır.

Özellikleri:

Pozitif yükten çıkar, negatif yüke girer.
Çizgiler asla kesişmez.
Yoğunluğu, alanın büyüklüğünü gösterir.
İki aynı yük arasında çizgiler dışa doğru itici görünür.
Zıt yükler arasında çizgiler, çekici bir şekil oluşturur.

Bu çizgiler, Coulomb yasasının görsel bir temsilidir.

15. Deneysel Kanıt ve Coulomb’un Torsiyon Terazisi

Coulomb yasası, deneysel olarak torsiyon terazisi ile ispatlanmıştır.

Coulomb, ince bir telin ucuna bağlanmış hafif bir küreyi kullanarak, diğer bir yükün oluşturduğu dönme açısını ölçtü.
Bu sayede kuvvetin uzaklığın karesiyle ters orantılı olduğunu kanıtladı.

16. Ortamın Etkisi (Dielektrik Sabiti)

Eğer yükler boşlukta değil de başka bir ortamda bulunursa, ortamın dielektrik sabiti (εᵣ) dikkate alınır.

Formül: F=14πε0εr∣q1q2∣r2F = \frac{1}{4\pi \varepsilon_0 \varepsilon_r} \frac{|q_1 q_2|}{r^2}F=4πε0εr1r2∣q1q2∣

Burada:

ε0=8.85×10−12 C2/N\cdotpm2\varepsilon_0 = 8.85 \times 10^{-12} \, \text{C}^2/\text{N·m}^2ε0=8.85×10−12C2/N\cdotpm2 (boşluğun permitivitesi)
εr\varepsilon_rεr: ortamın bağıl permitivitesi

Örneğin:

Hava için εr≈1\varepsilon_r \approx 1εr≈1
Su için εr≈80\varepsilon_r \approx 80εr≈80

Yani su gibi ortamlarda kuvvet çok azalır.

17. Coulomb Yasasının Uygulama Alanları

Coulomb yasası yalnızca ders konusu değildir; günlük yaşam ve teknolojide birçok uygulaması vardır:

Fotokopi makineleri (yüklü toner tanecikleriyle baskı)
Elektrostatik boyama (toz boyaların yüzeye yapışması)
Toz tutucular ve hava filtreleri
Yıldırımın oluşumu ve paratonerler
Atom çekirdeği içindeki kuvvetlerin modellenmesi

Tüm bu olaylarda, yüklerin birbirine uyguladığı Coulomb kuvveti etkilidir.

18. Günlük Hayattan Bir Örnek

Bir balonun saçınıza sürtüldüğünde duvara yapışması, Coulomb kuvveti ile açıklanabilir:

Balon sürtünme ile negatif yüklenir.
Duvar nötrdür, ancak yaklaştırıldığında etki ile kutuplaşır:
Duvarın yakın yüzü pozitif, uzak yüzü negatif olur.
Zıt yükler arasında çekim kuvveti oluşur.
Sonuçta balon duvara yapışır.

Bu olay, hem etki ile elektriklenmeyi hem de Coulomb kuvvetini göstermektedir.

19. Coulomb Yasasının Matematiksel Önemi

Coulomb yasası, elektrik ve manyetizma konularının temel taşıdır.
Bu yasa, daha sonra elektrik alan (Gauss Yasası), potansiyel fark, kapasitör, elektrik akımı ve elektrostatik enerji konularının temelini oluşturur.

Yani bu yasayı anlamak, ileride göreceğimiz tüm elektrik konularını anlamanın ilk adımıdır.

🔚 SONUÇ VE ÖZET

Elektriksel kuvvet, yükler arasında çekme veya itme şeklinde etki eder.
Kuvvetin büyüklüğü, yüklerin çarpımıyla doğru, uzaklığın karesiyle ters orantılıdır.
Yükler noktasal kabul edilirse formül geçerlidir: F=k∣q1q2∣r2F = k \frac{|q_1 q_2|}{r^2}F=kr2∣q1q2∣
Ortamın türü kuvvetin büyüklüğünü değiştirir.
Kuvvet her zaman iki yükü birleştiren doğru üzerindedir.
Aynı yükler iter, zıt yükler çeker.
Elektrik kuvveti, doğadaki en güçlü kuvvetlerden biridir.

🧩 Kısa Özet Maddelerle:

k=9×109 N\cdotpm2/C2k = 9×10^9 \, \text{N·m}^2/\text{C}^2k=9×109N\cdotpm2/C2
F∝q1q2F \propto q_1 q_2F∝q1q2
F∝1/r2F \propto 1/r^2F∝1/r2
Aynı yük → itme
Zıt yük → çekme
Boşlukta kuvvet maksimum, yalıtkan ortamlarda azalır.
Coulomb yasası, elektrik alan ve potansiyel konularının temelidir.