Matematik dersinin en görsel ve mantıksal yönü olan geometri, öğrencilerin hem analitik düşünme becerilerini hem de problem çözme yeteneklerini geliştiren önemli bir alandır. 10. sınıf 1. döneminde, öğrenciler geometriyi artık sadece şekil tanımakla değil, bu şekiller arasındaki ilişkileri yorumlamak ve ispatlamak düzeyinde öğrenirler. Bu dönem, lise matematiğinin temel taşlarından biridir.
🔹 Geometri Nedir?
Geometri, Yunanca “geo” (yer) ve “metron” (ölçü) kelimelerinden gelir; yani “yer ölçümü” anlamını taşır.
Başlangıçta sadece uzunluk, alan ve hacim hesaplamalarıyla ilgilenirken; zamanla doğrular, açılar, üçgenler, çokgenler ve daireler arasındaki ilişkileri inceleyen geniş bir bilim dalı haline gelmiştir.
Geometri, çevremizi anlamamızı sağlar. Bir köprü inşa edilirken, bir bina tasarlanırken, hatta bir futbol sahasının çizimleri yapılırken bile geometrik hesaplamalar kullanılır. Bu nedenle, 10. sınıf geometri konuları yalnızca okul için değil, günlük yaşamda da pratik bir değere sahiptir.
🔸 10. Sınıf 1. Dönem Geometri Konu Başlıkları
- sınıf geometri konuları, genellikle doğrular, üçgenler ve benzerlik üzerine kuruludur. Bu başlıklar ilerleyen yıllarda analitik geometri ve trigonometri konularının temelini oluşturur. İşte Milli Eğitim Bakanlığı müfredatına göre 1. dönemin ana konu başlıkları:
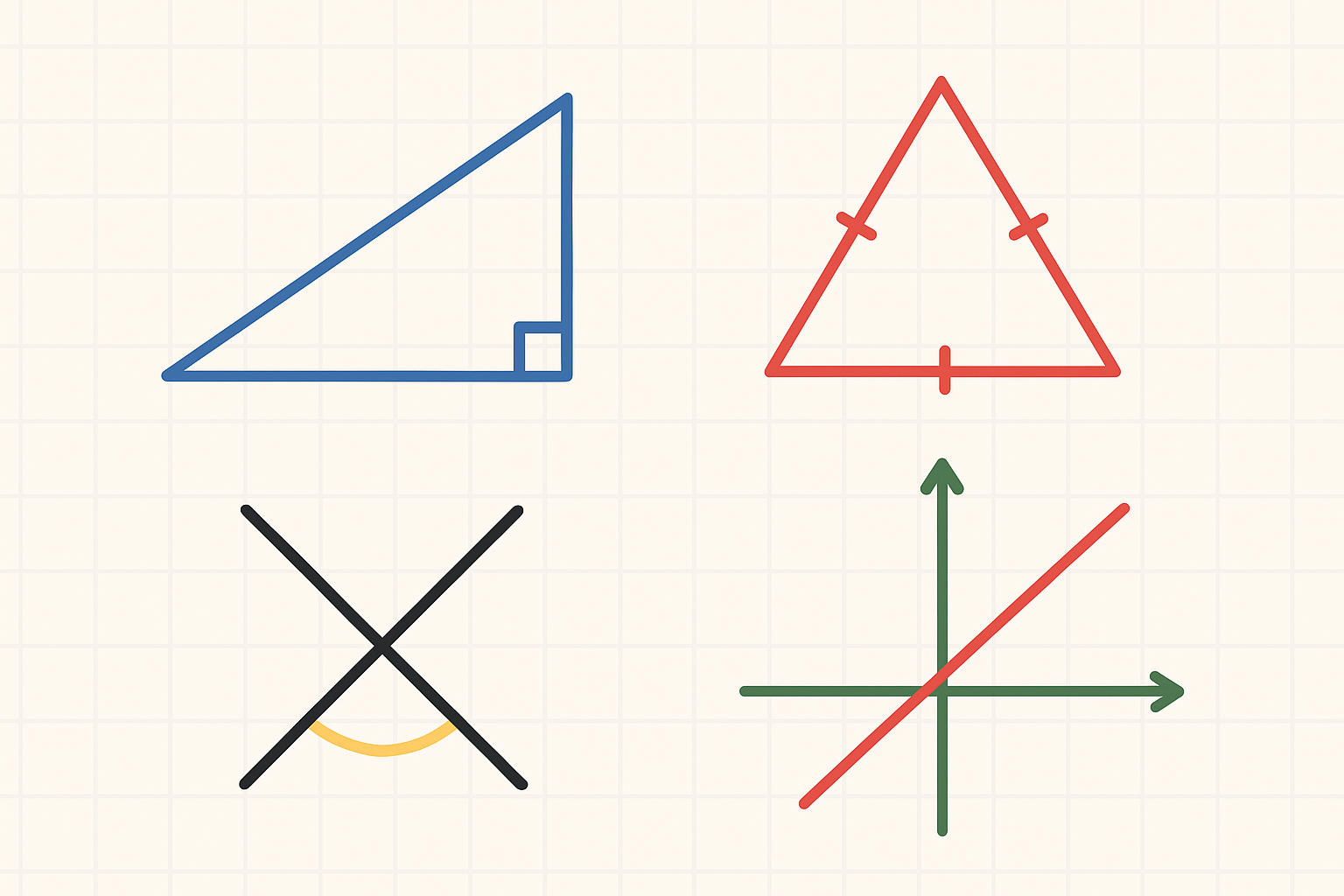
- Doğrular ve Açılar
- Üçgenler ve Özellikleri
- Eşlik ve Benzerlik
- Üçgenlerde Açı-Kenar İlişkileri
- Pisagor Teoremi ve Uygulamaları
- Üçgenin Alanı
Şimdi bu konulara tek tek ayrıntılı şekilde bakalım.
1️⃣ Doğrular ve Açılar
Bu ünite, geometrinin temel taşıdır.
Öğrenciler burada nokta, doğru, doğru parçası, ışın gibi kavramları öğrenir. Ayrıca paralel doğrular, kesişen doğrular ve bunlar arasında oluşan komşu, bütünler, ters, iç ters ve yöndeş açılar anlatılır.
🔸 İpucu: Açılarla ilgili sorularda her zaman paralel doğruları dikkatlice takip etmek gerekir. Çoğu soru, açılar arasındaki ilişkiyi fark etme becerisine dayanır.
Örnek:
Bir doğrunun üzerindeki açılar toplamı 180°’dir.
Paralel iki doğrunun arasında kalan iç ters açılar birbirine eşittir.
2️⃣ Üçgenler ve Özellikleri
Üçgenler, geometrinin kalbidir.
Bu konuda, öğrenciler farklı üçgen türlerini tanır: eşkenar, ikizkenar ve çeşitkenar üçgenler.
Ayrıca üçgenin iç ve dış açı özellikleri, kenar uzunlukları arasındaki ilişkiler detaylı şekilde işlenir.
🔸 Temel Bilgi:
Bir üçgenin iç açıları toplamı 180°, dış açıları toplamı ise 360°’dir.
Bir dış açı, kendisine komşu olmayan iki iç açının toplamına eşittir.
Örnek:
Bir üçgenin iç açıları 50°, 60° ve 70° ise, en büyük kenar en büyük açının karşısındadır.
3️⃣ Eşlik ve Benzerlik
- sınıf geometri müfredatında yer alan en önemli konulardan biri eşlik (congruence) ve benzerlik (similarity) konularıdır.
Bu konular, iki şeklin birbirine oranla nasıl aynı veya benzer olduğunu anlamamızı sağlar.
🔸 Eşlik:
İki üçgenin tüm kenar ve açıları birebir aynıysa bu üçgenler eştir.
Kısaltmalarla şöyle gösterilir:
- SSS Eşliği: Üç kenarı eşit olan üçgenler
- ASA Eşliği: İki açı ve aradaki kenar eşit
- SAS Eşliği: İki kenar ve aradaki açı eşit
🔸 Benzerlik:
İki üçgenin açıları eşit, kenar oranları ise orantılıysa bu üçgenler benzerdir.
Benzerlik oranı, benzer üçgenlerin büyüklük farkını gösterir.
Örnek:
Bir üçgenin kenarları 3 cm, 4 cm, 5 cm; diğerinin kenarları 6 cm, 8 cm, 10 cm ise bu üçgenler benzerdir (benzerlik oranı 2’dir).
4️⃣ Üçgenlerde Açı – Kenar İlişkileri
Bu bölümde öğrenciler, üçgenin açıları ile kenarları arasındaki matematiksel bağlantıları öğrenir.
En büyük açı, en uzun kenarın karşısındadır. Bu kural, birçok geometri sorusunun temelini oluşturur.
🔹 Üçgen Eşitsizliği:
Bir üçgende herhangi iki kenarın uzunlukları farkı, üçüncü kenardan küçük; toplamı ise üçüncü kenardan büyüktür.
Formül:
|a – b| < c < a + b
Bu formül sayesinde üçgen oluşturulup oluşturulamayacağı kolayca kontrol edilir.
Örnek:
a = 4 cm, b = 7 cm ise c uzunluğu 3 ile 11 arasında olmalıdır.
5️⃣ Pisagor Teoremi
Pisagor Teoremi, dik üçgenlerde kenar uzunlukları arasında kurulan çok ünlü bir bağıntıdır.
Teoreme göre:
a² + b² = c²
Burada c, üçgenin en uzun kenarı yani hipotenüs olarak adlandırılır.
🔹 Örnek:
a = 3 cm, b = 4 cm ise
c = √(3² + 4²) = 5 cm olur.
Pisagor teoremi yalnızca dik üçgenlerde geçerlidir, ancak diklik ispatı yapılırken de sıkça kullanılır.
6️⃣ Üçgenin Alanı
- sınıfta üçgen alanı hesaplamaları da detaylı şekilde öğretilir.
Alan formülleri, üçgenin verilen bilgilerine göre değişir.
🔸 Temel Alan Formülü:
Alan = (taban × yükseklik) / 2
🔸 İki kenar ve aradaki açı verilirse:
Alan = (1/2) × a × b × sin(C)
🔸 Heron Formülü:
Kenar uzunlukları a, b, c ise;
Alan = √[s × (s – a)(s – b)(s – c)]
(s = (a + b + c) / 2)
Örnek:
Kenarları 7, 8 ve 9 cm olan üçgenin alanı:
s = (7 + 8 + 9) / 2 = 12
Alan = √[12 × (12–7)(12–8)(12–9)] = √[12 × 5 × 4 × 3] = √720 ≈ 26.83 cm²
🔹 Geometri Çalışma Stratejileri
Geometri, sadece formül ezberlemekle değil, görselleştirme yeteneğiyle öğrenilir. İşte başarılı olmak için birkaç öneri:
- Çizim yapın. Her soruda şekli kendiniz çizin; bu, çözümün yarısıdır.
- Açı ve kenar ilişkilerini renklendirin. Farklı renk kalemlerle eşit açıları işaretleyin.
- Soruyu okurken zihninizde canlandırın.
- Sık tekrar yapın. Formüller unutulmaya müsaittir.
- Bol test çözün. Özellikle benzerlik ve eşlik konularında pratik yapmak çok önemlidir.
🔸 Geometri Neden Önemlidir?
Geometri sadece matematiğin bir parçası değil, mantık yürütme ve ispat yapma becerisinin geliştiği bir alandır.
Bir öğrenci geometrik ilişkileri çözebiliyorsa; soyut düşünme, analitik analiz yapma ve sistematik akıl yürütme yeteneği gelişmiş demektir.
Üstelik geometri, ilerideki üniversite sınavı (TYT-AYT) sorularında büyük paya sahiptir. 10. sınıfta öğrenilen konular, 11. ve 12. sınıf geometrisinin temelidir.
🔹 Sonuç
- sınıf 1. dönem geometri öğrenme alanı, öğrencinin analitik düşünme yeteneğini en çok geliştiren bölümlerden biridir.
Bu dönemde işlenen doğrular, açılar, üçgenler, eşlik, benzerlik ve alan hesapları hem günlük hayatta hem de üniversite sınavında öğrencinin işine yarayacak temel becerilerdir.
Geometriyi sevmek için onu anlamak gerekir. Şekilleri sadece çizim olarak değil, bir mantığın ifadesi olarak görmek, bu dersi keyifli hale getirir.
Her soru bir hikâye gibidir — çözümü bulmak ise hikâyenin sonunu yazmaktır.