12. Sınıf 1. Dönem Fizik
Ünite: Elektrik ve Manyetizma
Konu: Elektrik Devreleri – Seri ve Paralel Bağlantılar
⚡ 1. Elektrik Devresi Nedir?
Elektrik devresi, elektrik akımının bir kaynaktan çıkıp iletkenler aracılığıyla devre elemanlarından geçerek tekrar kaynağa döndüğü kapalı bir yoldur. Bir devrenin çalışabilmesi için kapalı olması gerekir. Eğer devre bir noktadan açık kalırsa akım akmaz.
Temel devre elemanları:
- Pil veya batarya (Gerilim kaynağı)
- İletken tel
- Direnç (R)
- Anahtar (S)
- Ampul, lamba, motor vb. yükler
🔌 2. Elektrik Akımı, Gerilim ve Direnç İlişkisi
Elektrik akımı (I), birim zamanda bir kesitten geçen yük miktarıdır.
Gerilim (V) ise akımı devrede iten potansiyel farkıdır.
Direnç (R) ise akımın geçişine karşı gösterilen zorluktur.
Bu üç büyüklük arasındaki ilişki Ohm Kanunu ile verilir: V=I⋅RV = I \cdot RV=I⋅R
- V: Gerilim (Volt)
- I: Akım (Amper)
- R: Direnç (Ohm, Ω)
Bu temel yasa hem seri hem de paralel devrelerin çözümünde kullanılır.
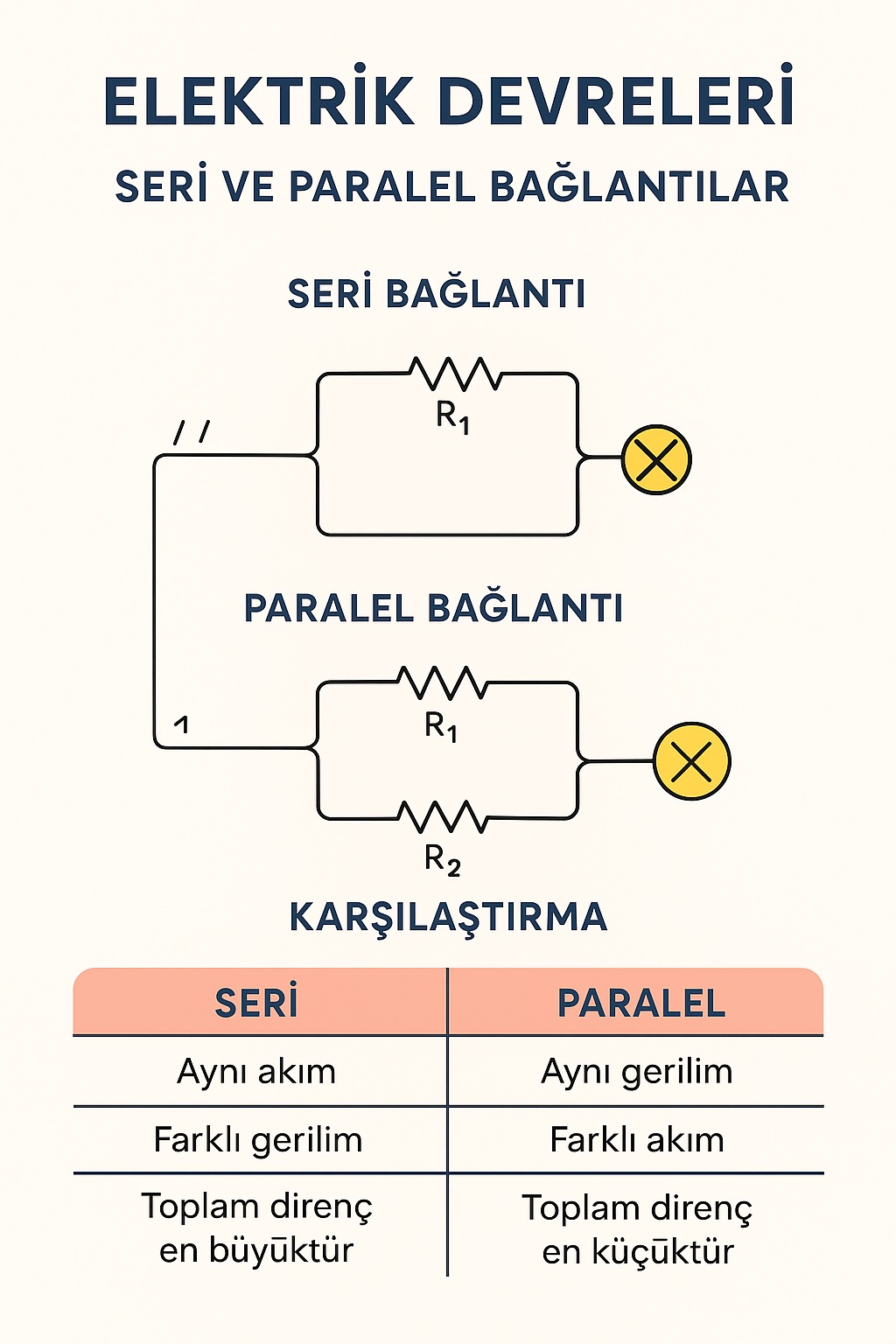
🔋 3. Seri Bağlantı
Tanım: Dirençlerin uç uca bağlanmasıyla oluşturulan devreye seri bağlantı denir.
a) Özellikler:
- Aynı akım her dirençten geçer. I1=I2=I3=II_1 = I_2 = I_3 = II1=I2=I3=I Çünkü devre tek bir yol içerir.
- Toplam gerilim, dirençler üzerindeki gerilimlerin toplamıdır: Vtoplam=V1+V2+V3V_{toplam} = V_1 + V_2 + V_3Vtoplam=V1+V2+V3
- Toplam direnç, dirençlerin toplamına eşittir: Rtoplam=R1+R2+R3R_{toplam} = R_1 + R_2 + R_3Rtoplam=R1+R2+R3
- Bir direnç arızalanırsa (koparsa) devrenin tamamı çalışmaz.
b) Örnek:
3 Ω, 4 Ω ve 5 Ω dirençleri seri bağlanmıştır.
Toplam direnç: Rt=3+4+5=12 ΩR_t = 3 + 4 + 5 = 12\ \OmegaRt=3+4+5=12 Ω
Eğer devreye 12 V’luk bir pil bağlanırsa: I=VRt=1212=1 AI = \frac{V}{R_t} = \frac{12}{12} = 1\ AI=RtV=1212=1 A
💡 4. Paralel Bağlantı
Tanım: Dirençlerin uçlarının birbiriyle aynı iki noktaya bağlanmasıyla oluşturulan bağlantıdır.
a) Özellikler:
- Gerilim tüm dirençlerde aynıdır: V1=V2=V3=VV_1 = V_2 = V_3 = VV1=V2=V3=V
- Toplam akım, dirençlerden geçen akımların toplamıdır: Itoplam=I1+I2+I3I_{toplam} = I_1 + I_2 + I_3Itoplam=I1+I2+I3
- Toplam direnç şu şekilde bulunur: 1Rt=1R1+1R2+1R3\frac{1}{R_t} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}Rt1=R11+R21+R31
- Dirençlerden biri kopsa bile diğerleri çalışmaya devam eder.
b) Örnek:
4 Ω ve 6 Ω dirençleri paralel bağlı. 1Rt=14+16=512⇒Rt=2,4 Ω\frac{1}{R_t} = \frac{1}{4} + \frac{1}{6} = \frac{5}{12} \Rightarrow R_t = 2,4\ \OmegaRt1=41+61=125⇒Rt=2,4 Ω
12 V gerilim uygulanırsa: I=122,4=5 AI = \frac{12}{2,4} = 5\ AI=2,412=5 A
⚙️ 5. Seri ve Paralel Devrelerin Karşılaştırması
| Özellik | Seri Devre | Paralel Devre |
|---|---|---|
| Akım | Aynı | Farklı |
| Gerilim | Farklı | Aynı |
| Toplam Direnç | En büyük | En küçük |
| Devre Koparsa | Tamamı çalışmaz | Diğer kollar çalışır |
| Kullanım Alanı | Sürekli akım gerektiren basit devreler | Ev devreleri, lambalar |
⚡ 6. Karışık (Bileşik) Devreler
Bazı devrelerde hem seri hem paralel bağlantılar bir aradadır. Bu tür devrelere bileşik devreler denir.
Bu devreleri çözmek için:
- Önce paralel kolların eşdeğer dirençleri bulunur.
- Daha sonra bu değerler seri dirençlerle toplanır.
- Son olarak Ohm kanunu uygulanır.
Örnek:
Bir devrede 6 Ω’luk iki direnç paralel, bunlara 4 Ω’luk bir direnç seri bağlanmış olsun. 1Rp=16+16=26⇒Rp=3 Ω\frac{1}{R_p} = \frac{1}{6} + \frac{1}{6} = \frac{2}{6} \Rightarrow R_p = 3\ \OmegaRp1=61+61=62⇒Rp=3 Ω
Toplam: Rt=3+4=7 ΩR_t = 3 + 4 = 7\ \OmegaRt=3+4=7 Ω
🧠 7. Voltmetre ve Ampermetre Bağlantısı
- Ampermetre akımı ölçer, seri bağlanır.
- Voltmeter gerilimi ölçer, paralel bağlanır.
Ampermetre direnci çok küçük, voltmetre direnci çok büyüktür.
💬 8. Enerji ve Güç Hesaplamaları
Elektrik devrelerinde enerji ve güç hesaplamaları şu şekilde yapılır:
- Güç (P): P=V⋅I=I2⋅R=V2RP = V \cdot I = I^2 \cdot R = \frac{V^2}{R}P=V⋅I=I2⋅R=RV2
- Enerji (E): E=P⋅tE = P \cdot tE=P⋅t
Burada
- P: Güç (Watt)
- E: Enerji (Joule veya kWh)
- t: Zaman (s)
Örnek:
Bir ampul 220 V gerilimde 0.5 A akım çekiyorsa: P=220×0.5=110 WP = 220 \times 0.5 = 110\ WP=220×0.5=110 W
1 saat çalışırsa: E=110×3600=396 000 JE = 110 \times 3600 = 396\,000\ JE=110×3600=396000 J
🔧 9. Seri ve Paralel Bağlantıların Günlük Hayattaki Önemi
- Seri bağlantı: Basit devre deneyleri, bazı pillerin bağlanması (örneğin fenerlerde).
- Paralel bağlantı: Ev elektrik sistemleri, prizler, lambalar, soketler.
Paralel sistemlerde bir cihaz bozulsa bile diğerleri çalışmaya devam eder. Bu nedenle evlerde paralel bağlantı tercih edilir.
🌐 10. Ohm Kanunu’nun Deneysel Uygulaması
Bir devre kurulur:
- Pil (gerilim kaynağı)
- Değişken direnç (reosta)
- Ampermetre ve voltmetre
Gerilim artırılarak akım ölçülür. V–I grafiği çizildiğinde doğrusal bir ilişki görülür.
Bu doğrusallık Ohm Kanunu’nu doğrular: R=VIR = \frac{V}{I}R=IV
🔍 11. Direncin Bağlı Olduğu Faktörler
Bir iletkenin direnci şu faktörlere bağlıdır:
- Uzunluk (l): Uzunluk arttıkça direnç artar. R∝lR \propto lR∝l
- Kesit alanı (A): Kalınlık arttıkça direnç azalır. R∝1AR \propto \frac{1}{A}R∝A1
- Madde türü (özdirenç ρ): R=ρlAR = \rho \frac{l}{A}R=ρAl
- Sıcaklık: Metallerde sıcaklık artarsa direnç artar.
🧩 12. Soru Tarzı Örnekleri
1️⃣ Seri Bağlantı:
2 Ω, 3 Ω ve 5 Ω dirençleri seri bağlanmıştır. 10 V’luk kaynak uygulanır.
Toplam direnç: 10 Ω I=1010=1 AI = \frac{10}{10} = 1\ AI=1010=1 A
Her bir dirençteki gerilim: V1=2V, V2=3V, V3=5VV_1 = 2V,\ V_2 = 3V,\ V_3 = 5VV1=2V, V2=3V, V3=5V
2️⃣ Paralel Bağlantı:
4 Ω ve 12 Ω paralel bağlı, 12 V gerilim uygulanmış. 1Rt=14+112=412⇒Rt=3 Ω\frac{1}{R_t} = \frac{1}{4} + \frac{1}{12} = \frac{4}{12} \Rightarrow R_t = 3\ \OmegaRt1=41+121=124⇒Rt=3 Ω
Toplam akım: It=123=4 AI_t = \frac{12}{3} = 4\ AIt=312=4 A
Her bir dirençten geçen akım: I1=3A, I2=1AI_1 = 3A,\ I_2 = 1AI1=3A, I2=1A
⚙️ 13. Seri ve Paralel Lamba Devreleri
- Seri bağlı lambalar: Akım aynı, biri patlarsa hepsi söner.
- Paralel bağlı lambalar: Her lamba kendi gerilimini alır, biri patlasa diğeri yanmaya devam eder.
📘 14. Uygulama Alanları
- Seri bağlantı: El feneri, batarya paketleri.
- Paralel bağlantı: Ev, ofis, okul elektrik tesisatı.
- Bileşik bağlantı: Elektronik devrelerde, karma sistemlerde.
🧮 15. Özet Formüller
| Büyüklük | Formül | Açıklama |
|---|---|---|
| Ohm Kanunu | V=I⋅RV = I \cdot RV=I⋅R | Gerilim–akım–direnç ilişkisi |
| Seri Direnç | Rt=R1+R2+…R_t = R_1 + R_2 + \dotsRt=R1+R2+… | Toplam direnç |
| Paralel Direnç | 1Rt=1R1+1R2+…\frac{1}{R_t} = \frac{1}{R_1} + \frac{1}{R_2} + \dotsRt1=R11+R21+… | Eşdeğer direnç |
| Güç | P=V⋅IP = V \cdot IP=V⋅I | Elektrik gücü |
| Enerji | E=P⋅tE = P \cdot tE=P⋅t | Harcanan enerji |
🧭
Elektrik devrelerinde seri ve paralel bağlantılar, akımın ve gerilimin nasıl dağıldığını anlamamızı sağlar. Bu bilgiler hem teorik fizik açısından hem de günlük yaşamda kullanılan elektrik sistemlerinin tasarımı açısından büyük önem taşır.
Elektrik devrelerinin doğru analiz edilmesi, enerji verimliliği, güvenlik ve cihaz performansı açısından da kritik bir rol oynar.